Sphere

This page is for discussions about true spherical maps, and the possibility of implementing something like this for Freeciv. True sphere means that the map is a sphere (you can pass over the poles), and that it is rendered as a three-dimensional sphere that is zoomed in sufficiently to present an almost flat surface.

Regular Icosahedron Tiled with Diamonds Solution[]

A regular icosahedron is a polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is the shape of the familiar 20-sided die. This shape has been used for map projections of Earth. See http://www.progonos.com/furuti/MapProj/Normal/ProjPoly/Foldout/Icosahedron/.

Each of the 20 faces can be subdivided into smaller triangles and then projected out onto a sphere. However, instead of having a sphere tiled with triangles, we want a sphere tiled with diamonds. Each triangle will be paired and combined with an adjacent triangle to form a diamond. Alternatively, this same result can be accomplished by first combining the original 20 triangles to form 10 diamonds then subdividing the diamonds and projecting them onto a sphere. See http://donhavey.com/blog/tutorials/tutorial-3-the-icosahedron-sphere/ for a tutorial on creating an icosahedron-based geodesic sphere.

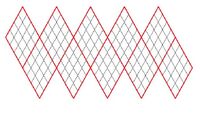
Icosahedron net tiled — Icosahedron net with diamond subtiles

A net of an icosahedron consists of 20 equilateral triangles. In order to facilitate using this net with existing resources, we will pair triangles and combine them into 10 diamond (rhombus) shapes. This will lay down the foundation for using an icosahedron to create a 3D map using existing diamond (or rectangle, or iso) shaped tilesets. The illustration on the right shows such a net that has been further subdivided by more diamonds.

Possible Tile Numbers[]

Each diamond can be evenly subdivided into any square number (e.g. 4, 9, 16...) of smaller diamonds. Since there are 10 diamonds, the number of tiles is always 10 * n^2, where n is a whole number.

	Square Dimensions	# of Tiles	Nearest Value for n	# of Tiles
Tiny	60x60	3600	n = 19	3610
Small	80x80	6400	n = 25	6250
Standard	100x100	10000	n = 32	10240
Large	140x140	19600	n = 44	19360
Huge	180x180	32400	n = 57	32490

Movement and cities[]

Icosahedron net tiled with indicators for irregularity — Tiles with more or less neighbors than normal have been colored blue or green, respectively.

Since the tiles are diamonds, the game play will be identical to rectangular maps except where the corners of the 10 large diamonds are. At these locations, some tiles will have 1 less neighbor (7 neighbors), and others will have 1 extra neighbor (9 neighbors). The north and south poles are the locations with extra neighbors. They have been marked blue on the diagram on the right. The tiles marked green are the tiles which will have less neighbors. Fortunately, this only affects 40 tiles total, regardless of the size of the map. Some cities that are built using affected tiles would not be shaped normally. Rules would have to be developed to determine which 21 tiles cities in these areas could use.

Icosahedron net tiled adjacent tiles — Selected tiles and their neighbors have been color coded.

Moving 'north' from one of the 5 northern-most tiles would be ambiguous. This ambiguity is because there is an extra tile at the North Pole. The player will need a way of expressing which of the possible tiles he intends to move to. North-west from that position could be well defined as the tile that is adjacent to the tile to the west. North east could similarly be handled. The South Pole has the same issue.

The above image on the left gives some examples of tiles that have more, less and the same number of neighbors as a tile in a rectangular map would. Gray and purple have 7 neighbors. Blue has 9 neighbors. Green and yellow have the usual 8 neighbors.

Icosahedron colored — Color coded Icosahedral sphere with diamond subtiles viewed from the north.

Icosahedron colored tilt — Icosahedral sphere with diamond subtiles with the equator in view.

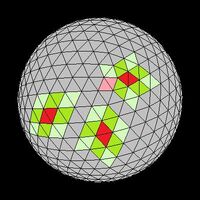
Icosahedron neighbors colored — Icosahedral sphere viewed from the north with selected subtiles and neighbors colored.

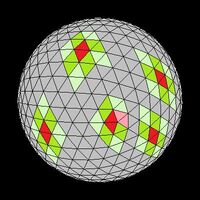
Icosahedron neighbors colored tilt — Icosahedral sphere with the equator in view with selected tiles and neighbors colored.

In order to visualize this in 3D, consider the following pairs of illustrations. The first image of each pair has the main diamonds indicated by color scheme. Individual subtiles have been paired into diamonds by using light and dark color. The next image is the same sphere, but has been colored to show a tile (red) and its neighbor tiles (light green, dark green, and light red). The light red tiles indicate where there is an extra neighbor or a missing neighbor tile in the cases where the main tile borders a corner of a main diamond. The first set of images on the left shows a view from the north, while the second set on the right shows more of the equator.

Coordinate system[]

Fortunately, since the tiles are diamonds, the coordinate system can be handled just as it would in a rectangular map (I presume this is done with a Cartesian coordinate system i.e. x & y value). Instead of there being just east-west map wrapping, every 'exposed edge' is wrapped to the corresponding edge to form the icosahedron.

Incremental Implementation from 2D map to 3D sphere[]

One of the nice features of this strategy is that we can implement it in phases. All of the game play and geometry and be worked out and implemented on a 2 dimensional net of an icosahedron. After this 2D implementation, the results can be mapped to a 3D sphere to complete the spherical game play experience.

Other possible subtilings[]

One obvious alternative is to tile each of the icosahedron's triangular faces with triangles. This solution presents a couple of obstacles to overcome.

A triangular tileset would have to be developed.

Rules for movement and cities would have to be developed.

Another possibility is to use a hexagonal tiling. However, this would necessarily create pentagons where the triangles of the icosahedron meet. Therefore, this solution would turn into the buckyball solution.

Rhombic Dodecahedron[]

Large diamonds of regular isometric tiles can be superimposed on the faces of a Rhombic Dodecahedron (http://en.wikipedia.org/wiki/Rhombic_dodecahedron ) The snag is that some tiles will have to be rotated relative to their neighbours, but on the plus side things are mostly the same as in a flat topology

Buckyball Solution[]

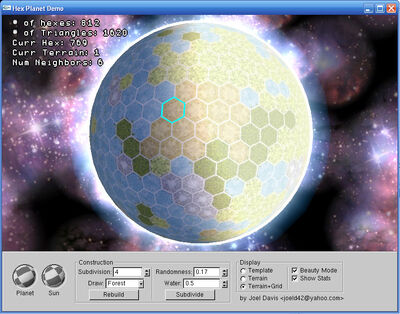
Hex planet demo by joel davis — A sphere made of hexagons and pentagons like a Buckyball. Notice the hexagons are tiled, but the are only single pentagons in the 'corners'. Source: http://vickijoel.org/hexplanet/

The solution discussed here assumes that the best way to implement this is a buckyball, a geodesic sphere with 12 pentagons and a variable number of hexagons. The smallest possible variant is a dodecahedron, with 12 pentagons and zero hexagons.

Problems[]

An algorithm to draw buckyballs with different numbers of tiles.
The best coordinate system to uniquely identify tiles.
An algorithm to identify a tile's neighbours.
Distance between two tiles (in real and square distance)

Drawing[]

You can draw buckyballs by constructing an icosahedron, then subdividing the triangles until you have a sufficient number, then by turning it into its dual, you have a buckyball.

A big challenge may be that aside from the dodecahedron, buckyballs created this way do not have regular polygons, that is, the tiles are not all the same size and shape. OpenGL can be used to stretch textures to fit, but this may not look good. Remains to be tested. Of course, since the buckyball consists of both pentagons and hexagons, we either have to have twice as many tiles, or we need to go over to some kind tile system that uses triangles (both pentagons and hexagons can be drawn as triangle fans).

Possible Tile Numbers[]

The buckyball sphere tiling is very adjustable. The number of tiles can be calculated by a simple equation: n = (x^2-1) * 10 + 12

In this equation x is the number of times the height of a hexagonal times can be fitted on one side of the original triangle. For example, if x is 1, the bucky-sphere has 12 tiles - it is a dodecahedron. If x is 2, the resulting bucky-sphere has 30+12 tiles - 30 hexagons and 12 pentagons. A bucky-sphere with x=16 has a total of 2562 tiles, roughly the number of tiles of a standard size map in Civilization III. If you take into account that in a spherical map with an earth-like appearance you will actually have polar ice-caps, you will of course "lose" some tiles to that. --Moriarty 12:49, 21 Jun 2006 (PDT)

Coordinate system[]

The crucial problem for a coordinate system on a sphere, as well as for finding distances between two tiles, is that while on a square map you know some things about the relationship between two tiles on any point on the map that you do not know for a sphere. For example, if you go N tiles north, N tiles east and N tiles south on a square map, the origin and the destination tiles are at N tiles distance to each other. This may not hold on a sphere, because the layout of tiles is not uniform the same way. At least this is my current working assumption. (Per 11:03, 20 Jun 2006 (PDT))

The coordinate system can be a spherical coordinates, which will give unique positions, but which does not guarantee to have tiles at each position. So (1,1,1) may be a tile but (2,1,1) may not be a tile. An alternative is to simply assign each tile a unique number. In either case we would probably have to keep a record of neighbours for each tile.

Sphere

Contents

Regular Icosahedron Tiled with Diamonds Solution[]

Possible Tile Numbers[]

Movement and cities[]

Coordinate system[]

Incremental Implementation from 2D map to 3D sphere[]

Other possible subtilings[]

Rhombic Dodecahedron[]

Buckyball Solution[]

Problems[]

Drawing[]

Possible Tile Numbers[]

Coordinate system[]

The buckyball project[]

Resources[]

Useful links[]

Previous Discussion Threads[]

Fan Feed